Wir denken uns die Kettenlinie auf folgende Weise angenähert (Abb. 3): An Fäden hängen Körper, die alle dasselbe Gewicht haben. Das Gewicht der Fäden ist verglichen mit dem Gewicht der Körper vernachlässigbar.  Die Abstände benachbarter Knoten sind alle gleich.

Die Fäden stehen unter Spannung, in ihnen fließt Impuls, dessen Richtung jeweils parallel zum Faden ist, und es gibt Verzweigungen (Knoten). Wir haben es also mit unterschiedlich gerichteten Impulsen in den Seilen zu tun. Das geeignete Mittel, diese Impulse zu beschreiben, sind daher Vektoren, die Information über Betrag und Richtung enthalten.

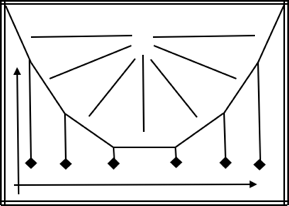
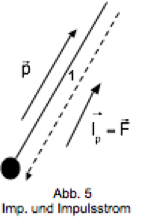
Abb. 4 ist ein Detail aus Abb. 3. Wir denken uns die Fäden im Knotenpunkt getrennt und am jetzt freien Ende einen Körper angebracht. Abb. 5 zeigt das für Fadenstück 1. Wenn die Spannung im Fadenstück erhalten bleibt, wird der Körper nach rechts oben beschleunigt (wenn kein Gravitationsfeld vorhanden wäre). Es fließt also der in Abb. 5 angegebene Impuls  in den Körper hinein. Richtung und Orientierung des  zugehörigen Impulsstromes werden durch den gestrichelten Pfeil dargestellt.

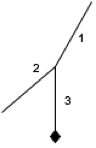
Durch Seil 1 fließt Impuls in den Knoten hinein, und da die Anordnung in Ruhe ist, fließt er durch Seil 2 und Seil 3 wieder heraus: Knotenregel. Die Seile haben unterschiedliche Richtungen und damit auch der in ihnen fließende Impuls. Es genügt daher nicht, die Beträge, der in den Fäden fließenden Impulse zu betrachten, auch die Richtung muss berücksichtigt werden.

Dazu ist es zweckmäßig, eine Zerlegung der auftretenden Impulse sowie deren Ströme in Komponenten bezüglich eines einmal festgelegten Koordinatensystems vorzunehmen. Ein solches ist in Abb. 3 bereits eingezeichnet. In diesem Koordinatensystem hat der Impuls  in Faden 1 die Komponenten        und       

(Abb. 6).

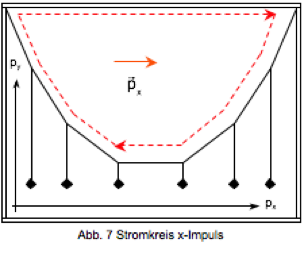
Die Knotenregel gilt für jede der beiden Komponenten. Durch Faden 1 fließen also sowohl „x-Impuls“ als auch „y-Impuls“ in den Knoten hinein und beide Impulssorten fließen auch wieder heraus. Dabei fließt durch Faden 3 nur y-Impuls und kein x-Impuls. Deshalb ist die Stromstärke des x-Impulses in Faden 2 gleich der des  x-Impulses in Faden 1, ja sie ist konstant in der ganzen Kette(nlinie).

Die Stromstärke des in Faden 2 fließenden y-Impulses, ergibt sich aus der in Faden 1 minus der in Faden 3. Die y-Stromstärke in Faden 3 ist aber nichts anderes als das Gewicht des angehängten Körpers.

Daraus ergibt sich für die Impulsströme in der Modellkette:

In jedem Teilstück der sich einstellenden Fadenlinie ist die Stromstärke des x-Impulses gleich groß. Es handelt sich um einem geschlossenen Stromkreis, zu dem auch die obere horizontale Traverse der Halterung gehört, die auf Druck belastet ist.

Wir gehen davon aus, dass die dadurch verursachte Verkürzung vernachlässigbar ist und damit auch die Strom des x-Impulses   durch die anderen Traversen.

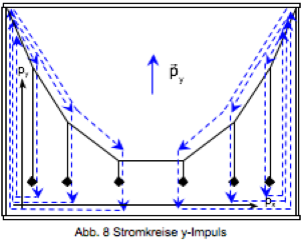
Die Stromstärke des y-Impulses ist in den beiden obersten an dem Gestell befestigten Teilen des Fadens am größten und entspricht in Abb. 3 u. 8  jeweils dem dreifachen Gewicht eines angehängten Körpers. Rechts oben beginnend nimmt sie von Teilstück zu Teilstück jeweils um das Gewicht eines Körpers ab. Der Impuls fließt durch die vertikalen Seilstücke und durch das Gravitationsfeld zur unteren horizontalen Traverse (und zur Erde) und durch die vertikalen Traversen des Gestells wieder nach oben. In der unteren Traverse stehen y-Impuls und Richtung des zugehörigen Impulsstromes senkrecht aufeinander, es herrscht dort eine Biegespannung.

Mit diesen Kenntnissen können wir die Frage nach der Form der Kettenlinie geometrisch in beliebiger Näherung beantworten.

Seilstücke und Vektor des darin fließenden Impulses sind parallel. Wir kennen also die Steigungen der Seilstücke, wenn wir die Impulsvektoren des in jedem Seilstück fließenden Impulses kennen.

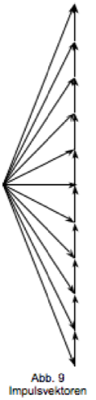
Die Impulsvektoren haben für jedes Seilstück dieselbe x-Komponente. Die y-Komponente nimmt von Seilstück zu Seilstück ab, wenn man die Linie von rechts nach links durchläuft. Der Betrag des jeweils von der y-Komponente zu subtrahierenden Vektors ergibt sich aus dem Gewicht der angehängten Körper.

Abb. 9 zeigt die Konstruktion der Impulsvektoren diesmal für 5 Körper (Maßstab willkürlich). Zur Konstruktion der Linie in Abb. 10 wurden die Steigungen aus Abb. 9 übernommen und auf gleich lange Seilstücke übertragen. Beginn rechts oben.

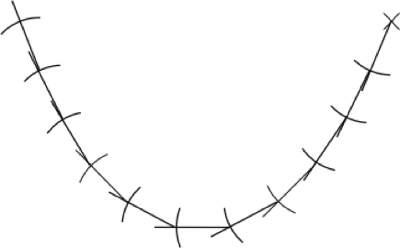
Abb. 10 Kettenlinie Näherung

Galilei war der Meinung, die Kettenlinie sei eine Parabel. Man sieht hier, dass das nicht richtig ist, denn bei einer Parabel ist die Steigung proportional zu x und nicht proportional zur Kurvenlänge. Bei einer Hängebrücke haben die vertikalen Seile alle denselben Abstand. Das durchhängende Tragseil hat also die Form einer Parabel, wenn man davon ausgeht, dass das Gewicht der vertikalen Seile im Vergleich zum dem der Fahrbahn vernachlässigbar ist. Es bleibt dem Leser überlassen, die entsprechende (Näherungs -) konstruktion auszuführen.

Abb. 11 zeigt den Vergleich von Kettenlinie und Parabel.

Man kann die Konstruktion auch für unterschiedliche Gewichte, wie es etwa bei Schmuckketten vorkommt, anwenden.

Die Frage nach der Form einer in der Schwerelosigkeit rotierenden Kette ist nicht so leicht zu beantworten.

Als Voraussetzungen wurden verwendet: gleiches Gewicht der Körper, gleicher Abstand der Knoten. Die Form der Linie ändert sich also nicht, wenn man Körper mit anderem Gewicht verwendet und auch nicht, wenn man die Anzahl der Körper erhöht. Durch Letzteres wird die Näherung verbessert.

Nun besteht eine Kette aus (starren) Kettengliedern und nicht auch masselosen Fäden mit angehängten Gewichten. Das tut der Argumentation aber keinen Abbruch. Wir denken uns exemplarisch ein Seilstück durch ein Kettenglied ersetzt, das das Gewicht eines der Modellkörper hat. Dadurch würde sich an der Linienform nichts ändern. Jetzt fließt über die ganze Länge des Stabes ebenso viel Impuls zur Erde wie vorher über des Seil ,an dem der Körper hängt.

(Abb. 12. Abb. 13)

Wenn nun Impuls in den Körper hineinfließt, gehört dazu die Information, wie viel Impuls pro Zeiteinheit fließt, also die Impulsstromstärke. Da Impuls ein Vektor ist, ist auch die Impulsstromstärke ein Vektor, der in traditioneller Sprechweise „Kraft“ genannt wird.

Die Richtung des Impulsstromstärkevektors (=Kraftvektors) kann als Richtung der Impulsänderung des Körpers oder dazu entgegengestzt vereinbart werden. In der Literatur werden beide Varianten verwendet..Wir entscheiden uns hier für:

Richtung Impuländerung = Richtung Impulsstromstärke = Richtung Kraft:

Es bleibt aber dabei, dass der in Abb. 5 eingetragene Impuls in den Körper hineinfließt.

Der Betrag der Impulsstromstärke kann mit einem Federkraftmesser gemessen werden, der Seilstück 1 ersetzt.

Da auch im hier betrachteten statischen Fall die Seile gespannt sind, fließen hier auch Impulsströme.