Die schwingende Seite
Für die Frequenz, mit der eine Saite eines Musikinstrumentes schwingt, gilt:
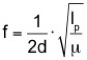
d: Abstand der Saitenenden, Ip: Betrag der Impulsstromstärke (Spannung) in der Saite, μ : lineare Massendichte (Masse pro Meter des Saitenmaterials).
Die Formel soll physikalisch begründet und in einem Experiment überprüft werden.
Die Bewegung einer Saite lässt sich mathematisch durch zwei aufeinander zu laufende Sinusfunktionen (Wellen) simulieren.
Simulation
Wir gehen aus von der horizontalen Ruheage der Saite. Die Saite steht unter Zugspannung, d. h. in der Saite fließt ein Impulsstrom. Impuls, der in die positive Richtung des gewählten Koordinatensystems weist, fließt nach links. Den Betrag der Stärke dieses Impulsstromes bezeichnen wir mit Ip.
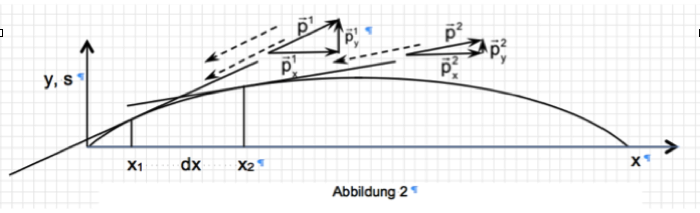
Impuls ist eine Vektor. Bei ausgelenkter Saite ändert sich die Richtung des in der Saite fließenden Impulses entlang der Saite. An jeder Stelle der Saite ist der Impulsvektor parallel zur Tangente an die Saite (Abbildung 2). Wir zerlegendie Vektor in seine Komponenten in x- bzw. y-Richtung. Durch eine ausgelenkte Saite fließen als x- und y-Impuls. Unter der Voraussetzung einer geringen Auslenkung ist die Stromstärke des x-Impulses näherungsweise unabhängig vom Ort und gleich der Stromstärke Ip der Ruhelage.
Die Stromstärke des y-Impulses ist ortsabhängig und aus Abbildung 2 ist ersichtlich: Aus dem Seilstück zwischen den Stellen x1 und x2 fließt bei x1 mehr y-Impuls heraus als bei x2 hinein.
Die Differenz der y-Impulsstromstärken an den Stellen x1 und x2 ist für die Beschleinigung (Impulsänderung) des (kurzen) Saitenstücks der Länge dx verantwortlich.
Die gestrichelten Pfeile gebenhit die Fließrichtung deer Impulskomponenten an. Sie sollen sich in Abbildung 2 auf den y-Impuls beziehen.
(Für die, es mathematischer mögen: Die Pfleile stellen das Vektorfeld der Impulsstromdichte dar.)
Nun ist der Betrag des y-Impulses, der aus dem Saitenstück herausfließt, größer als der Betrag des hineinfließenden. Laut Koordinaensystem fließt positiver y-Impunls aus dem Saitenstück heraus, das Stück wird als noch unten beschleunigt. Die Differenz der y-Stromstärken ist gleich
Mathematischer Hintergrund der Simulation
Gleichung der blauen Welle:
Gleichung der grünen Welle:
A: Amplitude, T: Schwingungsdauer, : Wellenlänge
Die Gleichung der schwingenden Saite erhält man durch addition der beiden Gleichungen.
Gleichung der roten Welle:
Alle diese Gleichungen sind Lösungen einer Differenzialgleichung, die sich hier leicht berechnen lässt. Die DGL ist einerseits eine mathematische Aussage. Sie zu kennen, ist zielführend, weil sie sich auch aus den physikalischen Gegebenheiten ableiten lässt (s. u.) und damit physikalische Größen zu den Parametern der Gleichung in Beziehung setzen lassen.
und
ist die Phasengeschwindigkeit der fortschreitenden Welle.
Mit der Frequenz
und dem Knotenabstand
lautet die Gleichung:
Nun wenden wir uns der Physik zu.
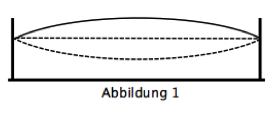
Abbildung 1 zeigt eine schwingende Seite, es handelt sich um eine Prinzipzeichnung für ein Monochord.
Schwingungsdauer, Wellenlänge und Ausbreitungsgeschwindigkeit der Wellen hängen von linearen Massendichte (Dicke der Seite) und der Spannung der Saite ab.
Die folgenden Überlegungen dienen der Aufklärung dieser Abhängigkeit (Abbildung 2).
also
Zwischen den Knoten, die den Abstand haben, bewegen sich die Punkte in Phase jedoch
mit unterschiedlicher Amplitude. Man nennt das eine "stehende Welle".
der Impulsänderung des Saitenstücks:
(Die oberen Indices beziehen sich beind Stelle x1 und 2, keine Exponenten)
µ bezeichne die lineare Massendichte, dann ist die Masse des Saitenstücks m = µ⋅dx und
Wenn man ausgeht von
an jeder Stelle der Saite,
Experimentelle Prüfung
als Saite wurde ein Draht verwendet. 0,935 m dieser Drahtes hatten die Masse 6,35⋅10-4 kg, also
dann gilt:
Der Vergleich mit
also lautet die Schwingungsdifferenzialgleichung
ergibt
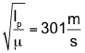
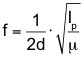
Spannung Ip = 61,4 N
Länge der schwingenden Saite d = 0,6m
f = 251 Hz
